L'addition des vitesses en relativité restreinte
La loi d'addition des vitesses relativiste, malgré sa forme peu intuitive, est en fait la seule qui puisse exister ! Et on peut le montrer sans même faire appel à l'idée de vitesse de la lumière...
Quand on découvre la théorie de la relativité restreinte, on nous assène presque immédiatement ces 2 faits :
La vitesse de la lumière est la même dans tous les référentiels.
Elle constitue une vitesse infranchissable.
Voilà qui est plutôt choquant et difficile à avaler ! La première objection qu’on a envie d’opposer, c’est une expérience de pensée très simple.
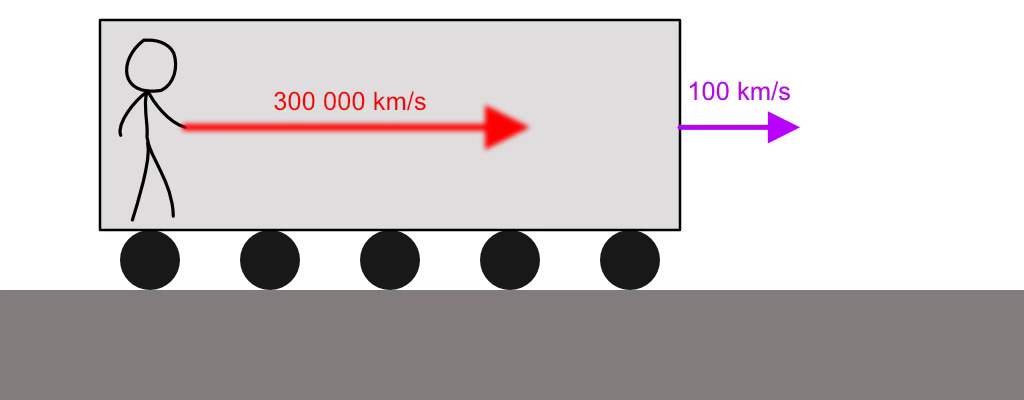
Si je dispose d’un pointeur laser dont la lumière va (pour simplifier) à 300 000 km/s, et que je me tiens dans un train qui va à 100 km/s par rapport au sol, alors la vitesse de la lumière du laser par rapport au sol devrait être de 300 000 + 100 = 300 100 km/s. Comment pourrait-il même en être autrement ?
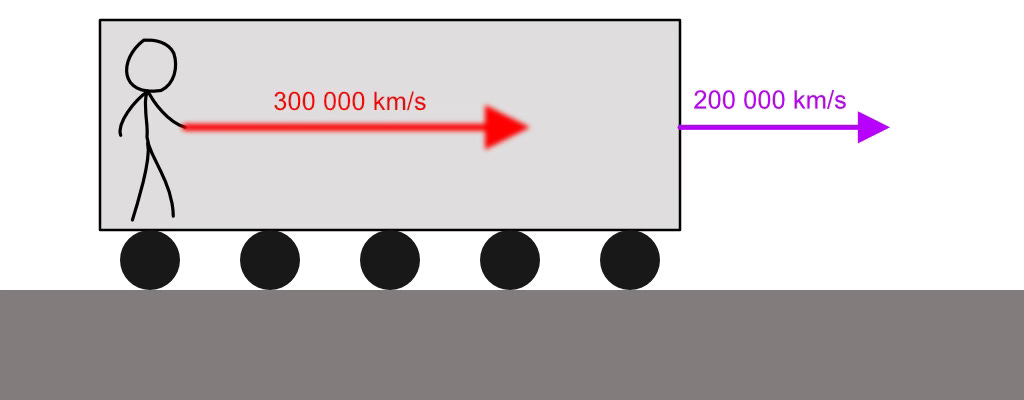
Et par extension, si je trouve un véhicule qui va suffisamment vite par rapport au sol, disons 200 000 km/s, une fois embarqué dans ce véhicule, la vitesse de la lumière de mon laser par rapport au sol devrait être de 500 000 km/s.
Donc on voit bien qu’on peut dépasser 300 000 km/s autant qu’on veut ! Non ?
La “bonne” addition des vitesses
Cette objection n’est bien sûr pas valide, et pour le comprendre, il faut réaliser qu’en relativité restreinte, on ne peut plus additionner naïvement les vitesses. Si un objet situé dans un train va à une certaine vitesse u par rapport au train, et que ce dernier va lui-même à une vitesse v par rapport au sol, notre objet n’ira en général pas à la vitesse u+v par rapport au sol. L’addition naïve des vitesses — que l’on utilise pourtant en physique newtonienne — est remplacée en relativité restreinte par une autre formule
où c est la vitesse de la lumière.
Examinons les conséquences de cette formule : son numérateur, c’est juste l’addition naïve. Mais puisque le dénominateur est supérieur à 1, cette formule nous dit que la vitesse de l’objet par rapport au sol sera toujours inférieure à celle qu’on obtient en faisant naïvement la somme u+v. Pour des vitesses très inférieures à c, le dénominateur sera proche de 1 et on retrouve la formule naïve, qui en pratique fonctionne suffisamment bien à nos échelles quotidiennes. Mais pour des vitesses très élevées, proches de celles de la lumière, l’addition naïve n’est plus valide.
Une autre conséquence de cette formule étrange, c’est que si l’objet dont on parle (celui qui se déplace par rapport au train) c’est justement de la lumière, alors on doit prendre pour sa vitesse u=c. Et on peut voir en appliquant bêtement la formule en remplaçant u par c que sa vitesse par rapport au sol sera alors
On retrouve la même valeur pour la vitesse de la lumière, indépendamment de la vitesse v de notre train ! Cette formule garantit que la vitesse de la lumière est bien la même dans tous les référentiels galiléens. Elle est invariante par changement de référentiel.
Très bien, mais d’où vient cette formule étrange ? Pourquoi est-elle la bonne ? Et pourquoi un phénomène aussi fondamental que la façon d’additionner les vitesses devrait dépendre de la vitesse de la lumière ? La théorie de la relativité est aujourd’hui au fondement de tous les phénomènes physiques (qu’il s’agisse de la relativité générale ou de toute la physique des particules via la théorie quantique des champs). Pourquoi la relativité restreinte devrait-elle se trouver liée à un phénomène physique en particulier, celui de la lumière ? Que vient faire l’optique ou l’électromagnétisme dans une formule fondamentale de mécanique ?
Une façon de le comprendre, c’est de se poser la question : Pourquoi l’addition des vitesses relativiste a-t-elle cette forme en particulier ? Pourquoi pas une autre ? Est-ce qu’une autre forme serait possible ? Si je veux, je peux en proposer plein, là comme ça. Par exemple :
Pourquoi pas celle-ci ? Existe-t-il un monde possible dans lequel cette formule est la bonne ?
Eh bien dans ce billet, nous allons voir qu’en fait, non : il n’aurait pas pu en être autrement ! La formule relativiste d’addition des vitesses est la seule permise, dès que l’on admet un ensemble très restreint de principes physiques simples. Et plus étonnant : on peut le montrer sans faire appel à la notion de lumière, et sans considérer son invariance comme un postulat de base.
Petite précision pour les connaisseurs : ce que je vais vous présenter ici est une démonstration que je n’ai jamais vue nulle part ! Elle est certes proche de démonstrations existantes permettant de construire le groupe de Lorentz, et c’est comme ça que je l’ai trouvée. Mais je n’ai jamais vu cet argument sous cette forme, et je trouvais intéressant d’en donner une approche qui se focalise uniquement sur la composition des vitesses plutôt que sur le groupe de transformation.
Déconstruisons l’addition naive des vitesses
Pour commencer, essayons de comprendre comment il est possible d’avoir une autre loi que la loi d’addition « naïve ». Celle-ci semble tellement naturelle, presque obligatoire sur le plan mathématique. Comment peut-il exister un monde dans laquelle on n’a plus forcément le droit d’écrire u+v ?
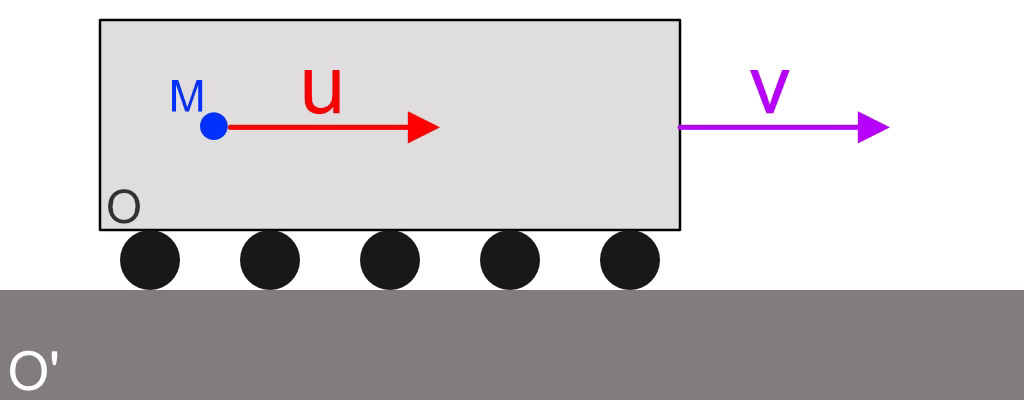
Pour cela examinons une situation concrète et essayons de comprendre pourquoi le raisonnement naïf n’est pas toujours correct. Prenons donc un objet (disons une bille) que l’on va noter comme un point M, et qui se déplace dans un wagon; wagon lui même en mouvement par rapport au sol.
Appelons u la vitesse de la bille par rapport au wagon, et v la vitesse du wagon par rapport au sol. Pour clarifier les choses, notons O un point du wagon qui va nous servir d’origine pour ce référentiel, et O’ l’origine du référentiel du sol.
La position de la bille par rapport au sol, c’est le vecteur O’M (dans la suite j’écrirai par commodité les vecteurs sans la flèche). Et donc la vitesse de la bille par rapport au sol, c’est la dérivée temporelle de ce vecteur O’M. Or on peut toujours écrire O’M = O’O + OM, il s’ensuit que la vitesse u’ de la bille par rapport au sol est
Le premier terme du membre de droite n’est autre que la vitesse du wagon par rapport au sol
Et le second est simplement la vitesse de la bille par rapport au wagon
Donc on a bien que u’, la vitesse de la bille dans le référentiel du sol, est égale à u+v, ...et donc les vitesses s’additionnent ! Comment pourrait-il en être autrement !?!
Vous vous en doutez, il y a une faille dans ce raisonnement, mais elle est subtile. Ici on suppose implicitement que le temps est le même dans les deux référentiels. Or en toute rigueur, on doit distinguer t’ le temps dans le référentiel du sol, et t le temps dans le référentiel du wagon. La vitesse de la bille dans le référentiel du sol s’obtient en dérivant par rapport à t’
Le premier terme du membre de droite est bien v, la vitesse du wagon dans le référentiel du sol, mais le second n’est pas la vitesse de la bille dans le référentiel du wagon. Pour cela il faudrait dériver par rapport à t, pas par rapport à t’.
On voit donc qu’à partir du moment où t et t’ ne sont plus reliés par un simple décalage temporel constant (ce qu’on supposait implicitement en relativité galiléenne / newtonienne), l’addition naive des vitesses n’a plus lieu d’être !
Cette petite clarification opérée, peut-on comprendre pourquoi l’addition des vitesses a la forme qu’elle a en relativité restreinte ? A savoir
Dans la suite du billet, comme je l’ai annoncé plus haut, nous allons démontrer qu’il s’agit de la seule forme admissible, et qu’aucune autre forme n’aurait été possible. Et pour cela on va s’appuyer uniquement sur quelques hypothèses élémentaires, qui n’ont absolument rien à voir avec la lumière, ni même avec son existence !
Hypothèse 1 : L’espace et le temps sont homogènes
Reprenons notre bille et notre train, et considérons donc deux référentiels : celui du train (noté R) et celui du sol (noté R’). En relativité, on appelle événement un point de l’espace-temps. Dans un référentiel donné, un événement est repéré par ses coordonnées, c’est à dire à la fois par une position x et un temps t : les coordonnées d’un événement dans un référentiel, c’est un couple de valeurs (x,t).
Les référentiels R et R’ étant différents, cela signifie que les coordonnées spatio-temporelles d’un événement donné ne seront pas les mêmes dans chacun de ces deux référentiels. Pour deux référentiels donnés, il existe toujours la possibilité de changer de référentiel, c’est-à-dire calculer les coordonnées (x’,t’) d’un évènement dans R’ en fonction des coordonnées (x,t) dans R.
En pratique, cela signifie qu’il existe deux fonctions F et G telles que
Notez bien que ces fonctions dépendent des deux référentiels R et R’. En pratique, il faudrait le faire figurer dans la notation. Mais pour simplifier, je vais simplement écrire F et G.
(Notez aussi que dans toute la suite je me contenterai d’une seule coordonnée d’espace x, mais cela n’entrave pas la validité du raisonnement)
Si l’on dispose d’un objet dont la trajectoire dans le référentiel R’ est x’(t’), sa vitesse est simplement la dérivée de sa coordonnée spatiale x’ par sa coordonnée temporelle t’. A partir des deux définitions reliant (x’,t’) à (x,t), on peut calculer la dérivée de x’ par rapport à t’.
Le calcul n’a rien de compliqué, c’est juste de l’application basique des calculs de dérivées partielles et des lois de composition des dérivations. Le moyen le plus direct, c’est de calculer les différentielles
Et de diviser les deux. En simplifiant en haut et en bas par dt, on obtient
(Si vous n’aimez pas cette méthode utilisant les différentielles, vous pouvez aussi dériver de façon pédestre l’ensemble, ça revient au même).
Une fois là, on observe que si l’on connait la vitesse u=(dx/dt) d’un objet dans le référentiel R, on peut déduire la vitesse u’=(dx’/dt’) dans le référentiel R’. Les deux vitesses sont donc liées par la relation
Dans cette expression, nous voyons 4 dérivées partielles. Les fonctions F et G étant des fonctions de x et t, a priori ces 4 dérivées partielles dépendent elles aussi de x et t. Mais si c’était vraiment le cas, cela voudrait dire que la formule de transformation des vitesses dépendrait du point de l’espace-temps où l’on se trouve.
Or cette éventualité contreviendrait au principe d’homogénéité de l’espace et du temps ! L’espace et le temps sont homogènes, et donc les lois fondamentales de la physique ne peuvent dépendre du point de l’espace et du temps auquel on se trouve.
Pour que la formule ne dépende pas du point d’espace-temps, il est nécessaire que ces 4 dérivées partielles soient en réalité des constantes. Il existe donc 4 nombres alpha, beta, gamma et delta, tels que :
Maintenant, quand je dis qu’il s’agit de constantes, cela signifie qu’elles ne dépendent pas de x ou de t. Mais souvenez vous que les fonctions F et G étaient spécifiques du changement de référentiel que l’on opère. Donc les constances dépendent a priori du couple R et R’. Voyons ce que l’on peut dire de plus précis en invoquant un nouveau principe : celui de relativité.
Hypothèse 2 : Le principe de relativité
Le principe de relativité nous dit que les lois de la physique sont les mêmes dans tous les référentiels galiléens, et que ceux-ci sont en translation rectiligne uniforme les uns par rapport aux autres. Nos 4 “constantes” ne peuvent donc dépendre que de la vitesse relative des référentiels. Si elles dépendaient du choix particulier de ces référentiels, cela signifierait que les lois de la physique ne seraient pas identiques dans différents référentiels galiléens. Pour deux référentiels en translation rectiligne uniforme l’un par rapport à l’autre, avec une vitesse v, nos 4 “constantes” sont donc des fonctions de v. On a donc de façon générale :
A ce stade de l’analyse, nous voyons que la simple utilisation du principe d’homogénéité de l’espace et du temps, couplée au principe de relativité, a déjà très fortement contraint les formes possibles pour la loi de transformation des vitesses. Entre deux référentiels, la loi d’addition des vitesses ne peut pas avoir de forme autre que celle que nous venons de trouver : le quotient de deux fonctions affines de u, les coefficients ne pouvant dépendre que de la vitesse de translation relative v.
Mais l’on peut aller beaucoup plus loin !
Les référentiels les uns par rapport aux autres
Dans l’expression ci-dessus, imaginons que u vaille 0, c’est-à-dire que l’on regarde le mouvement d’un point fixe du référentiel R, disons son origine. Puisque le référentiel R est en translation rectiligne uniforme de vitesse v par rapport à R’, alors la vitesse de ce point dans R’ doit être v. Donc si u=0, nécessairement u’=v. En substituant cette condition dans la formule ci-dessus, on obtient l’égalité
Mais nous savons également que l’espace est isotrope, le même dans toute les directions. Et l’on peut donc tenir le raisonnement symétrique : si l’on a un point fixe dans R’ (disons son origine), alors il aura une vitesse -v dans le référentiel R. En substituant u’=0 pour u=-v, on a donc
Il nous suffit d’écrire la nullité du numérateur pour extraire
En la combinant avec la première égalité ci-dessus, on tire
On peut donc éliminer beta et delta de notre loi d’addition des vitesses, et ne conserver que alpha et gamma
En divisant en haut et en bas par alpha, et en définissant
on obtient la forme générique
Nous avons à nouveau considérablement réduit les possibilités. Maintenant, on voit que la loi de transformation des vitesses ne peut prendre que la forme ci-dessus, où f(v) est une fonction a priori indéterminée. Mais l’on peut encore contraindre à nouveau sa forme à l’aide d’une dernière idée.
L’associativité de l’addition des vitesses
Pour cela imaginons le scénario suivant : notre bille va à la vitesse u dans le référentiel R du train, qui lui même se déplace à vitesse v dans le référentiel R’ des rails. Mais imaginons que ces rails soient eux-même fixés sur un porte avion se déplaçant à vitesse w par rapport à la côte, qui constitue le référentiel R’’. Ca a l’air compliqué ? Faisons un dessin !
Notre objectif va être d’exprimer u’’, la vitesse de la bille par rapport à la côte, et ce de deux façons différentes.
D’un côté, la vitesse u’ de la bille dans le référentiel du porte avion est donc obtenue par “addition” des vitesses
Mais le porte avion allant à vitesse w par rapport à la côté, la vitesse de la bille par rapport à la côte peut s’écrire à partir de u’ comme
Et donc en exprimant u’’ en fonction de u
Cette expression semble un peu lourde, et n’est pas dans la forme finale qui nous intéresse, mais pour l’instant gardons la telle quelle. On y reviendra.
Par ailleurs, on peut estimer la vitesse de cette bille par rapport au sol d’une autre manière. Notre bille va à la vitesse u dans le référentiel du train. Maintenant calculons la vitesse du train par rapport au sol. Puisque ce dernier va à vitesse v par rapport au porte avion, qui va lui-même à vitesse w par rapport à la côte, le référentiel du train par rapport au sol va donc à la vitesse
En appliquant à nouveau notre formule d’addition des vitesses à cette vitesse et à la vitesse u de la bille, on peut également écrire pour la vitesse de la bille par rapport au sol
Voyons cette expression comme une fonction de la variable u. Elle est ici naturellement sous une forme intéressante du type
Pour faciliter la comparaison avec l’expression précédente que nous avons obtenue plus haut, mettons cette dernière sous la même forme. Le calcul est direct mais il faut y aller sans se tromper : il faut d’abord multiplier en haut en bas par (1+f(v)u) puis diviser en haut et en bas par (1+f(v)w). Allez pour les ronchons du fond je vous mets le calcul
A l’issue de cette manipulation on obtient un truc qui a l’air assez peu lisible
Mais l’avantage, c’est que nous avons donc deux expressions de u’’ sous la même forme, et obtenues par deux routes différentes. On peut les voir comme deux fonctions de u sous la forme d’un quotient de fonctions affines : écrivons l’identité des deux dénominateurs.
Ca a l’air compliqué, mais ce sont simplement deux fonctions affines de u ! Commençons par identifier les deux termes constants, on tire
En manipulant cette expression on a
Nous avons ici à droite une fonction qui ne dépend que de w (et donc indépendante de v) et à gauche l’inverse. Il s’agit donc d’une constante indépendante à la fois de v et w, notons là k.
On a donc de façon générale que f est une fonction linéaire
On peut ensuite aisément vérifier que cette forme permet de satisfaire également l’autre terme de notre identité des deux dénominateurs, ainsi que l’identité des numérateurs.
C’est presque la fin du voyage ! A ce stade, nous avons donc à nouveau contraint un peu plus la forme possible de l’addition des vitesses. Celle-ci ne peut être que de la forme
où k est une constante. Pour des raisons dimensionnelles, celle-ci est homogène à l’inverse du carré d’une vitesse. Posons pour simplifier la constante
Notez qu’à ce stade C est juste une constante homogène à une vitesse, je ne préjuge pas de sa signification ! On voit que notre loi de transformation est nécessairement de la forme
Avec cette forme, on remarque que C correspond à une vitesse qui serait invariante par changement de référentiel.
Finalement, nous avons déduit que les lois possibles pour l’addition des vitesses sont très limitées : elles doivent forcément être de cette forme et faire intervenir une constante C, qui représente une vitesse invariante…ou presque !
Notez que quand j’ai défini C par rapport à k, j’ai escamoté une possibilité : celle où k serait simplement égal à 0. Si c’est le cas, cela correspond en quelque sorte à C infini, et on retrouve la loi d’addition naive valable en relativité galiléenne.
Ce que nous montre cette petite analyse, c’est qu’une fois prises en compte les nécessités d’homogénéité, d’isotropie et le principe de relativité, il n’y a que deux formes possibles pour la loi d’addition des vitesses :
soit la forme naïve, auquel cas il n’existe pas de vitesse invariante
soit la forme que nous avons trouvé, auquel cas il existe une vitesse invariante C.
Manifestement, nous vivons dans un univers où c’est la deuxième possibilité qui est réalisée. Il existe une vitesse invariante, qui se trouve être (entre autres) celle de la lumière. Mais on a pu arriver à cette forme sans avoir besoin d’invoquer de prime abord l’invariance de la vitesse de la lumière, l’expérience de Michelson-Morley ou ce genre de choses.
Bonus pour les connaisseurs
Certains d’entre vous auront certainement reconnu des arguments similaires à ceux que l’on invoque pour démontrer que le groupe de Lorentz (et son cas “dégénéré”, le groupe de Galilée) sont les seuls groupes de transformation de l’espace-temps qui satisfont à la fois l’homogénéité, l’isotropie et le principe de relativité.
Mais je trouvais intéressant de chercher une démonstration “parallèle” qui travaillerait uniquement sur la loi de composition des vitesses. Bien sûr, la portée en est moindre (puisque la loi de composition se déduit du groupe de transformation), mais cela me semble être un exercice intéressant, et légèrement plus simple à mon goût que le raisonnement au niveau des groupes. Pour ceux que ça intéresse, on peut retrouver cet argument dans
Lee, A. R., & Kalotas, T. M. (1975). Lorentz transformations from the first postulate. American Journal of Physics, 43(5), 434-437.
et même sous une forme encore un peu plus générique dans
Lévy-Leblond, J. M. (1976). One more derivation of the Lorentz transformation. American Journal of Physics, 44(3), 271-277.







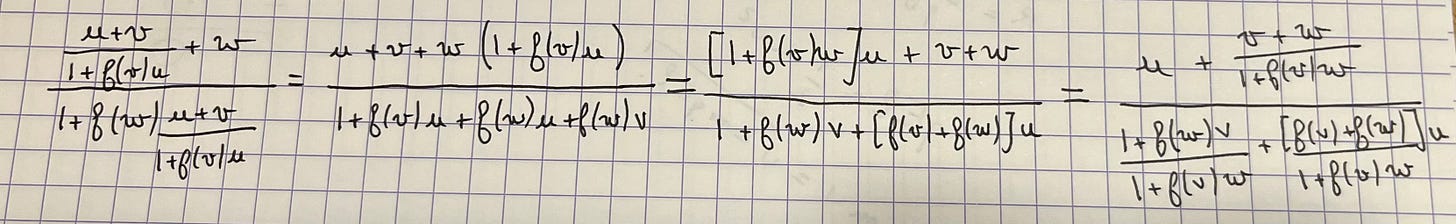
Je suis tombé sur une conférence dont la présentatrice suggérait que la déformation du temps et de l'espace pouvait être différents. Et qu'elle attendait les observations du satellite Euclid pour conclure.
Gemini me dit que le résultat de l'expression (c + v) / (1 + (cv / c²)) n'est pas toujours égal à c !
Exact ou faux ?