Qu'est-ce qu'une corrélation forte ? [Stats, ép. 1]

La notion de corrélation est régulièrement abusée, souvent critiquée...et parfois injustement ! Comment s'y retrouver ?

On ne compte plus le nombre de fois où une corrélation statistique est invoquée dans un débat, bien trop souvent sans le recul et la contextualisation nécessaire. A tel point que c’est devenu un sport sur les réseaux sociaux de marteler en retour « corrélation ne signifie pas causalité » ou de se moquer en dégainant les infographies du site Spurious correlations, qui montre par exemple un excellente corrélation entre le taux de divorce dans l’état du Maine, et la consommation par personne de margarine :

On a aussi régulièrement l’appel à ce cartoon d’XKCD qui brocarde les corrélations ridicules

« Je ne fais pas confiance aux régressions quand il est plus difficile de deviner le sens de la corrélation, que d’y trouver une nouvelle constellation”.

Et pourtant, est-ce que se satisfaire d’une corrélation qui affiche fièrement

\(R^2=0.06\)

c’est nécessairement ridicule ?

On va essayer de faire un peu la lumière là-dessus aujourd’hui. Les habitués des outils statistiques n’y apprendront sans doute pas grand chose, mais ce billet devrait être le premier d’une série consacrée à ces questions statistiques !

Jouons au basket

Pour illustrer les différentes notions que l’on va aborder, je vais me servir d’un exemple. Un exemple fictif, certes, mais je trouve que le meilleur moyen de bien comprendre ce qu’il se passe, c’est d’appliquer les méthodes statistiques sur des données dont on sait exactement ce qu’elles contiennent. Vous pouvez d’ailleurs retrouver tous mes calculs (Python) sur mon github.

Imaginez que je collecte les résultats d’un test de performance administré à un grand nombre de joueurs de basket, et que pour chaque joueur je mesure sa taille (en cm) et son score moyen au test (score qui s’étale en principe entre 0 et 100).

Je dipose donc d’un tableau de ce genre

Je n’ai affiché qu’une dizaine de lignes, mais imaginons que le tableau soit beaucoup plus long : 10000 individus. Premier réflexe, traçons le nuage de points !

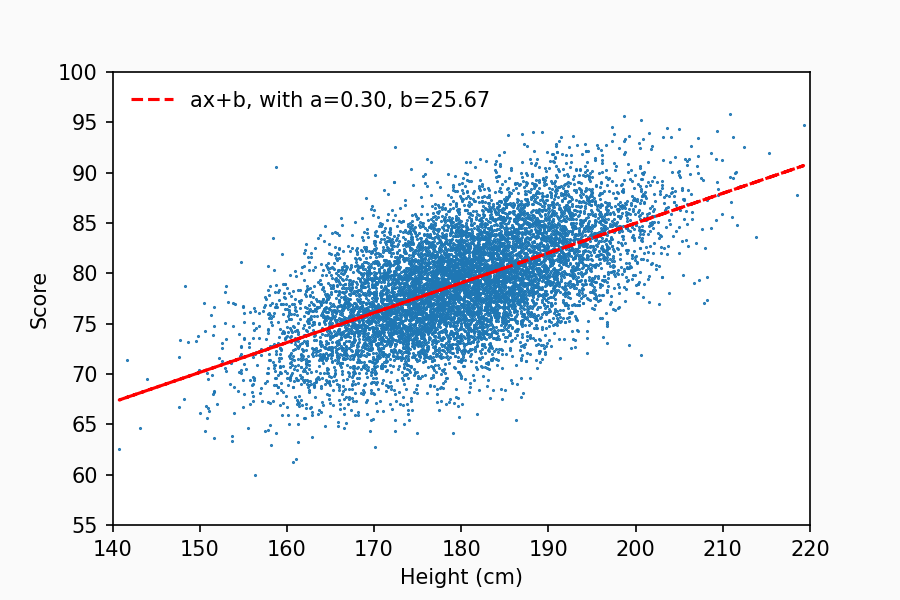
Youpi ! Une corrélation entre la taille et le score au test ! Je peux calculer le coefficient de corrélation associé (généralement noté “r” ou “rho”), et on trouve une valeur de 0,6. Pas mal, mais qu’est-ce que ça signifie au juste ? S’agit-il d’une corrélation qu’on peut qualifier de forte ?

Pour essayer de le préciser, on peut calculer et afficher la droite de régression linéaire :

Tout ceci est fort sympathique, on peut lire que “a”, le coefficient directeur de la droite de régression est égal à 0,30. Cela nous renseigne semble-t-il sur la force de l’association entre la taille et le score, en nous disant qu’une taille d’1 centimètre supplémentaire est associée en moyenne à un score 0,3 points plus élevé. Mais attention, il ne faut pas confondre coefficient directeur et coefficient de corrélation ! Le coefficient directeur vient avec une unité, ici des “points par cm”, alors que le coefficient de corrélation est sans unité, et toujours compris entre -1 et 1 (mais les signes des deux coefficients sont les mêmes, indiquant le signe de la corrélation).

La difficulté avec le coefficient directeur de la droite de régression, c’est que son interprétation va dépendre du contexte : est-ce que 0,3 points supplémentaires c’est beaucoup ? Imaginez que votre médecin vous dise : « Si vous prenez tel médicament, votre rapport albumine/créatinine baissera d’environ 1mg/mmol.» Pour interpréter cette indication, vous avez besoin de connaître quelles sont les variations typique du rapport albumine/créatinine, afin de savoir si le faire varier d’1mg/mmol c’est beaucoup, ou pas. Avec le coefficient directeur, c’est la même chose, il faut pouvoir le lier aux variations typiques de la cible, pour savoir si la régression nous apprend quel que chose d’utile ou d’insignifiant.

Le plus souvent, la mesure qui est rapportée pour juger de la qualité d’une régression, c’est le fameux “R carré”, qu’on appelle parfois le coefficient de détermination (dans la suite je vais parfois le noter R^2 car Substack n’autorise pas encore les exposants) Sa valeur dépend du modèle que l’on choisit d’ajuster à nos données. Dans le cas de notre simple régression linéaire, le R^2 n’est autre que le carré du coefficient de corrélation (mais notez qu’on utilise “petit r” d’un côté et “grand R” de l’autre).

Le R^2 pour un modèle linéaire est donc en principe compris entre 0 et 1, et on le voit fleurir à tort et à travers sur le web et dans les présentations Powerpoint, du fait qu’Excel permet de le calculer et de l’afficher automatiquement

Une belle corrélation ? Eh non, “Beer’s law” ça ne parle pas de binouze mais de la loi de Beer-Lambert, qu’alliez vous imaginer !?

Mais pourquoi le R^2 ? Qu’est-ce qu’il signifie vraiment, et pourquoi l’utiliser plutôt qu’autre chose ? D’autant qu’il n’est pas très aidant : puisqu’il est ici le carré d’un nombre compris entre -1 et 1, sa valeur a tendance à être beaucoup moins flatteuse que celle du coefficient de corrélation ! Dans mon exemple ma corrélation intéressante de 0,6 devient un R carré de seulement 0,36 ☹️.

Pour comprendre ça, on va revenir à nos données.

Gauss à la rescousse

Avant de vouloir tracer des nuages de points et calculer des corrélations, regardons attentivement nos données. Commençons par les tailles des joueurs, et traçons un histogramme. On voit qu’on a une belle courbe en cloche, autrement appelée distribution gaussienne :

La moyenne est à 180cm, et l’écart-type est de 10cm. L’écart-type quantifie notamment la (demi-)largeur de l’histogramme à la moitié de sa hauteur (c’est le trait pointillé noir). Pour une distribution gaussienne, 68% des données se trouvent à moins d’un écart-type de la moyenne, et 95% à moins de deux écarts-types de la moyenne (entre les traits gris foncés et gris clairs respectivement).

On peut faire la même chose avec le score obtenu au test, et même constatation : c’est une bonne distribution gaussienne, ici de moyenne 79, et d’écart-type 5.

Une façon assez élégante de lier ces observations à notre nuage de point, c’est de faire apparaître les histogrammes sur les côtés.

Cela permet de visualiser à la fois la corrélation, mais aussi la distribution des hauteurs (en haut) et des scores (à droite) qui engendrent cette corrélation.

Jusqu’ici, je vous ai surtout parlé d’écart-type, mais il existe une autre quantité importante en statistiques : la variance. La variance, c’est tout simplement le carré de l’écart-type. Rien de très compliqué à part que son interprétation est plus délicate puisque c’est un carré. Si l’écart-type est donné en kg ou en €, la variance sera en “kg au carré" ou en “€ au carré”, ce qui n’est pas très simple à se représenter physiquement. Mais pourquoi diable alors utiliser la variance plutôt que l’écart-type ? Eh bien c’est simple, les variances s’ajoutent !

Plus précisément si vous avez une variable X qui est la somme de deux variables indépendantes X1 et X2, alors la variance de X sera la somme des variances de X1 et X2. Mais ça ne marche pas avec les écarts-types, eux ne s’ajoutent pas ! Ainsi la somme d’une gaussienne d’écart-type 3 et d’une gaussienne d’écart-type 4 n’aura pas un écart type de 7, comme on aurait pu l’imaginer, mais de seulement 5

\(\sigma(X) = \sqrt{\sigma(X_1)^2+\sigma(X_2)^2} = \sqrt{3^2+4^2} = 5\)

Donc la variance, c’est certes pas super parlant, mais ça s’ajoute, et c’est pour ça qu’on l’aime. On va y revenir !

Analyse par tranche

Revenons à notre écart-type sur le score obtenu au test (environ 5 points) : une façon de l’interpréter, c’est de le voir comme une forme de quantification d’incertitude. Si je désigne un joueur au hasard dans mon échantillon, vous ne connaissez pas son score au test a priori, mais vous savez qu’il y a 95% de chance qu’il soit entre 66 et 88 (à deux écarts-types de la moyenne).

Maintenant imaginez que j’aie effectivement tiré un joueur au hasard, mais que je vous communique sa taille : il fait 185cm ! Qu’est-ce que cela change sur votre estimation de son score au test ?

On peut s’en faire une idée en restreignant nos données autour de 185cm.

On voit que l’histogramme des scores (à droite) est un peu plus resserré que ce qu’il était sur l’ensemble des données. On peut notamment calculer l’écart-type sur ces données restreintes, et on trouve seulement 3.97, là où on avait 5 sur l’ensemble de l’échantillon. Avec notre modélisation linéaire, la connaissance de la taille permet de réduire l’écart-type (l’incertitude) sur le score.

Je viens de le faire sur une petite tranche de joueurs autour de 185cm, mais on peut répéter la procédure sur d’autres tranches, et ainsi calculer “l’écart-type par tranche de taille”, voici le résultat en fonction de la tranche :

On retrouve de façon consistante un écart-type résiduel d’environ 4 dans chaque tranche, inférieur à l’écart-type global de 5. Il s’agit donc de “l’écart-type quand on connait la taille”.

On peut reformuler ça avec les variances au lieu des écarts-types, en élevant les valeurs au carré : la variance résiduelle est d’environ 16, là où la variance initiale était de 25. Le fait de connaitre la taille a permis de réduire la variance de 9 sur un total de 25. Avec l’information de taille du joueur, on a donc expliqué 9/25 = 36% de la variance totale des données. Or ce 36%, c’est justement le “R^2” qu’on a trouvé tout à l’heure !

Et voilà pourquoi on s’attache autant à cette mesure du R^2, c’est qu’elle représente la part de variance expliquée par le modèle linéaire, et donc quantifie de manière tangible la force de l’association entre les deux variables : à quel point connaître une des variables (par exemple la taille) nous renseigne sur l’autre (le score au test).

Le dessous des données

Pour bien vous expliquer comment tout cela fonctionne, je vais vous montrer comment j’ai créé les données que vous avez vues. Je partagerai mon code sur Github, mais voici les lignes qui ont servi à les créer :

Comme vous le voyez, la hauteur est comme prévu une distribution gaussienne de moyenne 180 et d’écart-type 10, et le score est la somme d’un terme qui dépend linéairement de la hauteur (avec un offset et un coefficient) et d’un bruit gaussien.

Souvenez vous que les variances s’ajoutent ! La variance totale du score est donc la somme de deux composantes : la composante linéaire offset + coefficient * height qui “hérite” de la variance de la taille (et qui est donc la part “expliquée” par la taille) et la composante résiduelle noise * … (qui représente toutes les autres influences sur le score). C’est parce que les variances s’ajoutent qu’on peut parler de la proportion de variance expliquée (et qu’on ne peut pas le faire avec les écarts-types, même si ce serait plus simple à interpréter).

On peut dans le code comparer les valeurs théoriques et mesurées de la variance totale et de la part de variance expliquée, et s’assurer que l’interprétation est correcte. La variance expliquée est égale à la variance de la hauteur multipliée par le carré du coefficient directeur de la relation linéaire.

Je résume : si on dispose d’un coefficient de corrélation r, on peut essayer d’interpréter sa signification quantitativement en l’élevant au carré : il représente alors la part de variance expliquée, le R^2, par l’application d’un simple modèle linéaire.

Appréhender les corrélations

Le coefficient de corrélation (et son carré) sont donc une mesure de la taille de l’effet que l’on cherche à estimer, c’est-à-dire de la force de l’association entre nos deux variables. J’ai choisi pour l’exemple un cas où on a très envie de voir une causalité (entre taille et score au basket), mais souvenez-vous que tout ce qu’on raconte ici reste valide qu’elle que soit la nature de la relation causale.

Mais si demain on m’annonce un coefficient de corrélation de disons r=0,5 (R^2 de 25%), comment puis-je lui donner du sens ? Le psychologue et statisticien américain Jacob Cohen a proposé une échelle qualitative en suggérant de considérer une corrélation de r=±0.1 comme faible, ±0.3 comme moyenne et ±0.5 comme grande.

Mais il peut aussi être utile d’ancrer ces valeurs dans des références qui nous donnent une perception intuitive. Par exemple :

• entre le poids et la taille chez les humains, on a un coefficient r=0.44.

• entre la latitude et la température moyenne d’une ville (aux USA), r=0.6.

• entre le succès critique et et le succès commercial d’un film, r=0.17.

Meyer en a compilé toute une liste (voir aussi ACX) :

Meyer, G. J., Finn, S. E., Eyde, L. D., Kay, G. G., Moreland, K. L., Dies, R. R., ... & Reed, G. M. (2001). Psychological testing and psychological assessment: A review of evidence and issues. American psychologist, 56(2), 128.

Cela permet de montrer à la fois que même avec un coefficient qui semble élevé (supérieur à 0.5), ça ne veut pas dire, loin de là, qu’il n’y a pas d’autres facteurs. Inversement, un coefficient de moins de 0.2 peut nous dire quand même quelque chose d’intéressant et potentiellement utile.

Mais pour bien illustrer les rapports entre coefficient de corrélation et R^2, j’aimerais tout de même vous présenter un exemple étonnant de cas où il faut être prudent…et ne pas jeter le bébé corrélation avec l’eau du bain du coefficient r !

L’aspirine est-elle efficace pour le coeur ?

En 1987, une grosse étude (randomisée et en double aveugle) a été réalisée sur plus de 22000 personnes pour étudier l’impact de l’utilisation de l’aspirine sur la réduction des crises cardiaques. Le résultat de l’étude ? Un coefficient de corrélation de 0.03, et donc un carré d’à peine 0.01. Ridicule, non ?

Et pourtant sachez que cette étude a dû être arrêtée prématurément pour des raisons éthiques, tant l’impact positif du traitement était énorme ! Poursuivre l’expérience aurait été considéré comme trop défavorable à l’intérêt du groupe contrôle, qui ne recevait qu’un placebo.

Mais comment est-ce possible avec un coefficient de corrélation de 0.03 ? Eh bien voici les résultats bruts (source en légende)

Rosenthal, R. (1995). Progress in clinical psychology: Is there any?. Clinical Psychology: Science and Practice, 2(2), 133.

Pas de doute sur l’effet, il y a quasiment deux fois moins de crises cardiaques dans le groupe traité par rapport au placebo (104 vs 189), et vu la taille de l’étude, le doute n’est pas permis !

Vous pouvez refaire le calcul si vous n’y croyez pas

Ce qu’il se produit, c’est qu’il est délicat d’interpréter une valeur de r dans le cas d’un ensemble très déséquilibré et ici avec des variables binarisées. Ici dans les deux groupes, la plupart des gens ne font pas de crise cardiaque. Et donc interpréter le carré du coefficient de corrélation comme une part de variance expliquée ne fonctionne pas car nous sommes très loin des hypothèses d’un modèle linéaire (pour ceux qui connaissent, on utiliserait plutôt un odds ratio, on en reparlera…)

D’ailleurs pour ce genre de cas, on ne parle pas franchement de coefficient de corrélation r mais du coefficient “Phi” (voir la dernière ligne du code) qui se calcule analytiquement à partir des 4 valeurs brutes. Numériquement, il a la même valeur, mais cela permet de souligner le fait qu’il ne faut pas l’interpréter de la même manière qu’un coefficient de corrélation dans une situation continue où tout est gentiment gaussien.

En conclusion

J’espère avoir bien fait la lumière sur les différentes quantités que l’on peut croiser. Le coefficient de corrélation, c’est comme l’écart-type ou la moyenne, c’est une quantité qu’on a toujours le droit de calculer sur les données, sans qu’il y ait des hypothèses à vérifier. En revanche, comme pour l’écart-type par exemple, l’interprétation de cette quantité va dépendre des détails (de la même façon qu’on ne peut interpréter l’écart-type avec la règle des “68% / 95% à ± 1 ou 2 écarts-type” que si la distribution est raisonnablement gaussienne.)

Et donc un coefficient de corrélation faible ne veut pas forcément dire qu’il ne se passe rien, surtout si on est loin d’un modèle linéaire. A contrario un coefficient fort ne veut pas dire que tout est déterminé, même r=0.6 n’explique qu’un tiers de la variance dans un modèle linéaire.

Le R^2, lui, se calcule toujours dans le contexte d’un choix de modèle : c’est précisément le coefficient de corrélation (au carré) entre la cible et la valeur régressée. Ici je n’ai fait que de la régression linéaire simple, donc c’est la même chose que le coefficient de corrélation entre les deux variables, mais on aurait pu faire plus compliqué (notez que le R^2 n’est pas stricto sensu “un carré”, et peut même en principe être négatif si on utilise un modèle plus pourri que le modèle linéaire !)

Dans les prochains épisodes, j’aborderai la question totalement éludée jusqu’ici : celle de la fameuse significativité statistique ! On parlera aussi peut-être de corrélation sur les rangs, d’information mutuelle et d’hétéroscédasticité (parce que j’aime bien le mot.)