Le plus gros hack de l'histoire du jeu vidéo (2/2)

Où l'on révèle le secret derrière la "racine carrée inverse rapide" de Quake III

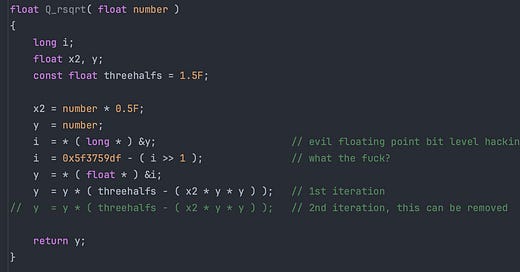
Dans le billet précédent, je vous ai présenté l’incroyable code découvert dans le code source de Quake III Arena, et censé calculer l’inverse de la racine carrée d’un nombre

Nous avions vu que cette technique était en fait une simple méthode itérative de Newton (voir les deux dernières lignes marquées “iteration”), combinée à une initialisation si performante qu’une seule itération devenait nécessaire.

Cette initialisation se fait notamment via cette ligne mystérieuse assortie de son commentaire fleuri

Aujourd’hui nous allons voir ce que fait cette ligne de code déroutante, ce que signifie la constante magique 0x5f3759df, et pourquoi on aurait presque pu, finalement, la découvrir nous-même ! Et pour cela, parlons de la façon dont un ordinateur stocke les nombres.

La représentation des nombres en mémoire

Commençons par les nombres entiers. Vous savez sans doute qu’un ordinateur ne sait fondamentalement manipuler que des 0 et des 1, des bits d’information, et que toute donnée est in fine stockée en mémoire de façon binaire.

Pour les nombres entiers, on va simplement les coder en base 2, par exemple la séquence de bits 00100101 correspond au nombre 37. Chaque bit représente une puissance de 2, et en lisant de droite à gauche, cette séquence vaut

\(1*2^0 + 0*2^1 + 1*2^2 + 0 *2^3 + 0 * 2^4 + 1*2^5 + 0 * 2^6 + 0 * 2^7\)

qui est le nombre 37.

Avec 8 bits (un octet), on peut représenter des nombres entre 0 et 255. Avec 16 bits, entre 0 et 65635, et avec 32 bits entre 0 et 4294967295. Bien sûr, on peut décider de représenter aussi des entiers relatifs, et interpréter une séquence de 8 bits comme un nombre entre -127 et +128. Le stockage sera strictement le même, c’est l’interprétation qu’on en fait qui va différer.

Pour les nombres décimaux (ou dits à virgule flottante), c’est plus compliqué. Ils sont classiquement stockés sur 32 bits. Mais comment ? Intuitivement on pourrait se dire que la partie entière est stockée par exemple sur 16 bits, et la partie décimale sur 16 bits, ou bien une autre répartition. Mais ça ne serait pas très efficace car ça limiterait beaucoup la capacité à représenter des nombres très grands ou très petits.

Une solution plus maline, c’est de s’inspirer de la notation scientifique, celle qui pour écrire le nombre 3742,17 va utiliser

\(3,74217 \times 10^3\)

L’avantage de cette notation, c’est qu’elle est parcimonieuse et permet de représenter à la fois des nombres très grands, mais aussi très petits si on utilise des puissances négatives de 10.

Eh bien les nombres à virgule flottante, c’est pareil, mais au lieu d’utiliser les puissances de 10, on va utiliser les puissances de 2, puisque les ordinateurs comptent en binaire. Ainsi on va écrire le nombre 3742,17 comme

\(1.82723114 \times 2^{11}\)

De façon générale, tout nombre réel peut s’écrire (approximativement) sous la forme

\(\pm r \times 2^E\)

où E est un exposant entier positif ou négatif, et r est un nombre compris entre 1 et 2. Ce point est important : dans la notation scientifique usuelle en base 10, on utilise une puissance de 10 que multiplie un nombre décimal compris entre 1 et 10, mais en base 2, ce nombre décimal est seulement compris entre 1 et 2.

On peut même réarranger légèrement la forme de l’écriture de la façon suivante : puisque ce préfacteur est entre 1 et 2, on peut le récrire sous la forme

\(\pm (1+m) \times 2^E\)

où le nombre m est entre 0 et 1.

C’est de cette notation que s’inspire la norme IEEE 754, qui définit la représentation des nombres flottants. Vous voyez que pour stocker un nombre en utilisant cette notation scientifique en base 2, il nous faut à la fois stocker le signe, l’exposant E et le nombre m. Pour les nombres flottants en simple précision, stockés sur 32 bits, voici comment ceci est réalisé : le premier bit représente le signe (0 pour +, 1 pour -), les 8 bits suivants servent à coder l’exposant, et les 23 bits suivants ce qu’on appelle la mantisse

Prenons un nombre réel codé de cette façon, comment le reconstituer ? Vous lisez les 8 bits de l’exposant, vous obtenez un nombre E entre 0 et 255, il faut ensuite lui retrancher 127 pour le ramener entre -127 et 128 et pouvoir coder les exposants négatifs.

Pour la mantisse c’est plus subtil, on lit 23 bits et on obtient donc en principe un nombre entier entre 0 et 2^23 -1. Puisqu’on veut obtenir un nombre m entre 0 et 1, il suffit de le diviser par 2^23. Cela signifie que quand on lit E et M, on reconstitue le nombre réel à partir de la formule suivante

\((1 + \frac{M}{2^{23}}) \times 2^{E-127}\)

(Pour les pros du sujet, je passe sous silence les questions de 0, NaN, nombre dénormalisés etc.)

Une compréhension intuitive de la formule magique

Imaginez que vous ayez un nombre réel stocké sous la forme d’une notation scientifique en base 2, par exemple le nombre

\(1.343567245 \times 2^{18}\)

et que je vous demande de trouver un ordre de grandeur de sa racine carrée ? Si on veut juste un ordre de grandeur rapide sans trop s’embêter, on peut juste laisser la partie décimale telle quelle, et diviser l’exposant par 2, et proposer par exemple

\(1.343567245 \times 2^{9}\)

Bien sûr ça n’est pas LA réponse, mais c’est un ordre de grandeur grossier, tout à fait acceptable…en particulier si l’on cherche un bon point de départ pour initialiser une méthode itérative de type Newton !

Faisons le même raisonnement avec la racine carrée inverse, il faut cette fois diviser l’exposant par 2, et prendre son opposé

\(1.343567245 \times 2^{-9}\)

Et c’est là que réside l’astuce de la racine carrée inverse rapide. En exploitant le stockage des nombres flottants selon la norme IEEE 754, on accède très facilement à un très bon point de départ pour la méthode itérative de Newton : il suffit de diviser l’exposant par 2 et de prendre son opposé !

Or dans les notations binaires, la division par 2 est une opération très simple, il suffit de décaler la représentation binaire vers la droite. Si vous avez le nombre 42, dont la représentation binaire est 00101010, vous virez le bit le plus à droite (c’est à dire vous décalez tout le monde vers la droite en réintroduisant un zéro à gauche), et vous obtenez le nombre 21.

En langage C, le décalage des bits d’un nombre vers la droite se fait à l’aide de l’opérateur >>. Je pense que vous y voyez maintenant un peu plus clair sur ce que fait la ligne de code mystère

On y voit l’expression - (i >> 1) qui traduit intuitivement l’idée de “Prendre l’opposé de l’exposant et le diviser par 2”. Mais malheureusement, les choses ne sont pas si simple et le diable se cache dans les détails.

Le premier détail qui nous aide à comprendre le sens de certaines autres lignes du code, c’est qu’il n’est pas permis en C de manipuler les bits d’un nombre à virgule flottante, et notamment d’effectuer un décalage vers la droite. C’est assez logique car les 32 bits sont séparés en trois champs différents — le signe, l’exposant et la mantisse — et ça semble ne pas avoir beaucoup de sens de faire un décalage vers la droite…mais c’est quand même ce qu’on va faire !

Les deux lignes qui se trouvent de part et d’autre servent à cela :

Le “evil floating point bit level hacking” a pour objectif de prendre un flottant, de ne pas toucher à sa représentation binaire et de récupérer le nombre entier qui correspond à cette même représentation binaire. Attention, ça n’est pas du tout la même chose que de “convertir” le flottant en entier, ce qui ferait un simple arrondi. On conserve la même représentation binaire, mais on manipule ça comme un entier, or sur les entiers on a le droit de faire un décalage vers la droite, puis la ligne suivante on refait l’opération inverse, on réinterprète le résultat comme un nombre flottant.

Mais il nous reste un problème à résoudre : que viens faire la constante magique 0x5f3759df dans l’affaire ? Eh bien il faut regarder exactement ce qu’il se passe quand on effectue l’opération - (i >> 1).

L’inverse rapide

Avant de regarder le cas de la racine carrée inverse, regardons un problème plus simple : l’inverse. Je vous donne un nombre flottant stocké selon la norme IEEE 754, je vous demande de me trouver rapidement une approximation de son inverse. Facile me dites vous, il suffit de prendre l’opposé de son exposant. Sauf que l’entier 8 bits qui se trouve stocké dans la représentation n’est pas l’exposant lui-même, mais l’exposant décalé de 127 ! Et c’est ça qui va tout compliquer.

Simplifions nous la vie, imaginons qu’on cherche l’inverse d’un flottant qui soit 2^P. La mantisse est nulle (on dirait du Julien Clerc) et l’exposant est 127+P. La réponse que l’on veut obtenir après avoir inversé, c’est 2^(-P), qui est représenté par un exposant 127-P. Vous voyez donc que pour passer de 127+P à 127 - P, il ne faut pas bêtement prendre l’opposé, mais prendre l’opposé et ajouter 254, car 127-P = 254 - (127+P)

Traduisons ça avec une manipulation sur le nombre entier qui correspond à cette représentation flottante. On veut ajouter 254 à l’exposant, sauf que celui-ci est représenté après les 23 bits de la mantisse (“après” au sens que son poids est plus fort), il faut donc ajouter non pas 254, mais le nombre entier

\(254 \times 2^{23}\)

de façon à “sauter” les 23 bits de la mantisse, et à bien aller écrire “sur” les bits de l’exposant.

Voici un petit bout de code qui fait ça pas à pas (mon code est dispo sur le GitHub)

Et en voici la sortie, qui permet de visualiser ce qu’il se passe bit à bit sur le nombre 2^3. Son exposant initial est 130 (127+3), après négation il devient 126, or c’est 124 (127-3) qu’on veut, et la constante magique permet de compenser le biais.

Bien sûr ici le résultat est exact car on a pris une puissance de 2, si on prend un nombre quelconque, vu qu’on a pas traité la mantisse on obtiendra seulement une approximation, par exemple ici avec le nombre 12

La racine carrée rapide

On peut faire la même chose avec la racine carrée rapide, on décale vers la droite pour “diviser par 2” l’exposant, mais il va falloir rectifier avec une constante magique à cause du décalage de 127.

Prenons le nombre 16 = 2^4, son exposant est 127+4=131, et on souhaite trouver le nombre 4=2^2, dont l’exposant est 129. Après décalage vers la droite (qui vaut division entière par 2), l’exposant 131 devient 65. L’opération correcter à effectuer est d’abord d’ajouter 127, puis de diviser le tout par 2. En n’oubliant pas qu’il faut “sauter” les 23 bits de mantisse, cela correspond donc à l’utilisation d’une constante magique 0x1FC00000, qui vaut

\(\frac{127}{2} \times 2^{23} = 127 \times 2^{22}\)

Voici un exemple bit à bit

La racine carrée inverse rapide presque optimale

Vous avez compris le principe, passons maintenant à la racine carrée inverse rapide. Vous pouvez faire le calcul du décalage correct à faire, on trouve une constante magique à ajouter de

\(\frac{3}{2} \times 127 \times 2^{23}\)

et voici deux exemples bit à bit

En hexadécimal, cette constante magique s’écrit 0x5F400000.

Mais c’est bizarre, c’est pas tout-à-fait la constante du code de Quake III

Elle sont très légèrement différentes. Celle que j’ai trouvée correspond à l’entier 1598029824 tandis que celle du code de Quake représente l’entier 1597463007. Pourquoi cette différence ?

Eh bien parce qu’on peut faire encore un peu mieux que ce que j’ai montré, en s’occupant un tout petit peu de la mantisse, qu’on a largement ignoré jusqu’ici.

La racine carrée inverse rapide optimale ?

Pour comprendre en quoi on peut très légèrement améliorer la constante magique, il faut se pencher en détail sur ce que signifie l’opération qu’on effectue lorsque l’on manipule les bits.

Considérons un nombre réel de la forme

\(a = (1+\frac{M}{2^{23}})2^{E-127}\)

Avec la norme IEEE 754, le nombre entier qui a exactement la même représentation binaire est le nombre

\(I(a) = E \times 2^{23} + M%\)

On a vu tout à l’heure que en gros faire des opérations arithmétiques sur cet entier (comme prendre l’opposé ou diviser par 2) revenait à faire des opérations arithmétiques sur l’exposant du nombre réel d’origine. Or cet exposant est en gros le logarithme en base 2 de notre nombre réel, puisque c’est la puissance auquel on élève le nombre 2.

Cela nous met sur la voie : le nombre I(a) semble très relié au logarithme en base de 2 de a. Pour préciser exactement ce lien, calculons le logarithme en base 2 de a et voyons à quoi il ressemble

\(\log_2(a) = \log_2(1+\frac{M}{2^{23}}) + E -127 \)

En comparant cette expression avec celle de I(a), on extrait (en substituant E) que

\(I(a) = 2^{23} \left(\log_2(a) - \log_2(1+\frac{M}{2^{23}}) + 127 \right) + M\)

C’est à dire que

\(I(a) = 2^{23} \left(\log_2(a) - \log_2(1+\frac{M}{2^{23}}) + \frac{M}{2^{23}} + 127 \right)\)

Regardez les deux termes au centre de la parenthèse. C’est de la forme - log2(1+x) + x. Or cette expression est nulle pour x=0 et x=1, et pas très loin d’être nulle entre les deux. On a log2(1+x) qui est “presque” égal à x entre 0 et 1 (même si contrairement à ce que j’ai pu écrire avant, ça n’est pas un développement limité !). Si on fait cette approximation, les deux termes se compensent, et on obtient

\(I(a) \approx 2^{23} \left(\log_2(a) + 127 \right)\)

Et je vous laisse vérifier que cette écriture permet de retrouver les constantes magiques qu’on a déduites. Par exemple si on veut trouver le nombre entier qui représente la racine carrée inverse de a, on veut

\(I(a^{-1/2}) \approx 2^{23} \left(\log_2(a^{-1/2}) + 127 \right) = 2^{23} \left(-\frac{1}{2}\log_2(a) + 127 \right)\)

et donc

\(I(a^{-1/2}) = \frac{3}{2}127\times 2^{23} - \frac{1}{2} I(a)\)

qui est exactement la manipulation qu’on a effectué avec “notre” constante magique.

Mais comment faire mieux ? Eh bien en essayant de faire un tout petit peu mieux quand on écrit l’approximation log(1+x) = x.

En pratique on va utiliser cette approximation pour des valeurs de x uniquement entre 0 et 1. L’approximation en prenant simplement x est exacte pour x=0 et x=1, mais elle est un peu sous-estimée partout ailleurs

On doit pouvoir faire un peu mieux avec un petit décalage d’abscisses, par exemple log2(1+x) = x + C

Ici sur le graphe, j’ai utilisé C=0.043, qui est considéré comme l’optimum. Maintenant si vous reprenez les calculs ci-dessus en utilisant log2(1+x) = x + C comme approximation, vous allez voir que ça ne change presque rien, à part que la constante magique devient maintenant

\( \frac{3}{2}(127 - C) \times 2^{23}\)

Ca ne fait pas une grosse différence car C est faible par rapport à 127, mais ça améliore un tout petit peu pour pas plus cher, en prenant une constante magique légèrement inférieure.

Conclusion

Et voilà, nous sommes au bout du voyage ! C’était long mais à travers ces deux articles, je voulais vraiment montrer tout le cheminement intellectuel qui permet de déduire cette méthode de racine carrée inverse rapide d’une façon presque naturelle.

Et d’ailleurs d’après la section historique de l’article Wikipédia correspondant, différentes variantes de la méthode ont été déduites avant que celle-ci ne soit amenée chez id Software. John Carmack a d’ailleurs toujours nié en être l’inventeur. La première version publiée que j’ai pu trouver date de 1997.

Je n’ai pas tout écumé mais je n’ai pas vraiment trouvé d’endroit où on trouve ainsi tous les détails de l’explication, c’est pour ça que j’ai voulu me faire la mienne, en écrivant les codes correspondants au passage (rappel : ils sont sur mon GitHub) et en montrant que la démarche n’était pas spécifique de la racine carrée inverse.