"Grokking" : les modèles d'IA sont-ils capables de piger ?

Ce phénomène étonnant, découvert récemment, pourrait changer notre compréhension de l'apprentissage et de la cognition dans les réseaux de neurones...

Ces dernières années ont été le théâtre de progrès spectaculaires en matière d’intelligence artificielle, notamment via les modèles de langage comme (Chat-) GPT, dont l’efficacité a même surpris les spécialistes. Et pourtant, on peut légitimement se demander ce que comprennent vraiment ces modèles. Sont-ils capable de penser comme nous, ou ne font-ils que remixer bêtement ce qu’ils ont ingurgité ?

Une critique — notamment formulée par Yann Le Cun — est que ces modèles seraient incapables de se forger un modèle mental de notre monde, puisqu’ils ne l’appréhendent que via des descriptions textuelles.

Mais début 2022, des chercheurs d’OpenAI ont mis en évidence un phénomène spectaculaire et totalement inattendu, qu’ils ont baptisé grokking, et qui apporte de nouveaux éléments à ce débat. Le grokking pourrait en effet révéler la façon dont certains modèles d’IA se forgent un modèle mental pertinent des données avec lesquelles on les entraîne. Et cela pourrait notamment avoir des répercusions sur notre capacité à comprendre ce qu’il se passe à l’intérieur de ces “boites noires” que sont les modèles de deep learning.

Pour celles et ceux qui pratiquent déjà le machine learning, un aspect surprenant du phénomène est visible de façon dramatique dans cette figure

L’image est issue de l’article qui a révélé le phénomène :

POWER, Alethea, BURDA, Yuri, EDWARDS, Harri, et al. Grokking: Generalization beyond overfitting on small algorithmic datasets. arXiv preprint arXiv:2201.02177, 2022.

Comme on peut le voir sur le graphique, après quelques centaines d’étapes d’entrainement, le modèle semble perdu dans un sur-apprentissage total. Mais de façon inattendue, après un million d’étapes, il se produit un phénomène spectaculaire de généralisation tardive. Stupéfiant !

Si vous ne faites pas de machine learning, il est fort probable que cette courbe ne vous parle pas particulièrement, et que le paragraphe ci-dessus vous semble totalement incompréhensible. Mais rassurez-vous, nous allons expliquer tout cela tranquillement, et creuser les dessous du phénomène; et surtout voir en quoi cela peut nous éclairer sur la façon dont les modèles d’IA essayent de se forger un modèle mental des données qu’on leur présente.

J’ai réussi à reproduire ce phénomène de grokking de façon minimale en utilisant Pytorch, je vous partage le code sur Github. Mais avant cela, voyons d’abord quelques éléments préliminaires sur le sur-apprentissage, ceux qui les connaissent déjà peuvent passer à la partie suivante !

Sur-apprentissage et généralisation

Imaginez un simple problème avec deux variables X et Y, dans lequel j’essaye de prédire Y en connaissant X. Voici les données :

Une option naturelle ici est de faire une régression linéaire :

Cela ne marche pas trop mal. Mais on peut améliorer le résultat, avec par exemple une régression quadratique :

C’est bien mieux ! Mais ça n’est encore pas parfait, la courbe ne passe pas parfaitement par les points. Alors pourquoi s’arrêter là ? Poussons le bouchon au maximum, et faisons une régression avec un polynôme de degré 9 !

Là c’est idéal, ça colle nickel avec tous les points ! Mais vous voyez certainement le problème : ce qu’il se passe entre les points semble totalement folklorique. Imaginons par exemple qu’entre temps j’aie collecté de nouvelles données (en vert ci-dessous)

Notre modèle ne marche plus du tout. La raison est qu’il était bien trop riche au départ, il collait bien trop aux données : il a donc fait du sur-apprentissage. Or le sur-apprentissage va à l’encontre de la capacité de généralisation. Il faut donc essayer de trouver un équilibre : un modèle suffisamment riche pour coller à peu près aux données, mais suffisamment robuste pour avoir une chance de se généraliser à de nouvelles données.

Pour arriver à cela, on adopte une technique simple : quand on rassemble des données initiales, on les sépare d’abord aléatoirement en deux. La première partie, l’ensemble d’entrainement (ici mes points en bleu), servira à entrainer le modèle. La seconde partie, l’ensemble de validation (mes points en vert) servira à tester si le modèle est effectivement capable de faire de la généralisation.

Pour correctement calibrer et entraîner le modèle qu’on utilise, il faudra donc surveiller sa performance sur les deux ensembles. Si la performance sur l’ensemble d’entrainement est excellente, mais qu’elle est médiocre sur l’ensemble de validation, c’est le signe d’un sur-apprentissage (c’est ce qu’il se passait avec mon polynome de degré 9).

Vous le savez, dans les modèles d’intelligence artificielle “modernes”, on utilise principalement des réseaux de neurones. Or ceux-ci nous offrent plusieurs moyens de s’assurer qu’on évite le sur-apprentissage. Premièrement, il faut choisir une architecture de réseau dont la taille soit proportionnée à la quantité de données dont on dispose, et à la complexité du problème à résoudre.

Ensuite on peut faire en sorte que les paramètres du réseau, les poids, ne prennent pas des valeurs trop élevées, ce qui est généralement le cas lors d’un sur-apprentissage. A cette fin, lors de l’apprentissage, on ajoute une pénalité liée à la magnitude des poids. L’objectif de la phase d’entrainement sera donc de trouver un paramétrage des poids du réseau de neurones qui permette de bien coller aux données d’apprentissage, tout en n’impliquant pas des valeurs des poids trop élevées.

Et enfin, en pratique, on surveille la performance du réseau au cours de son apprentissage, et on s’efforce d’interrompre celui-ci quand la performance sur l’ensemble de validation finit par se dégrader. Voici typiquement le genre de courbe que l’on trouve dans les cours sur le sujet. Elle montre l’évolution des performances au cours de l’entrainement.

On y voit qu’au départ, la performance sur les deux ensembles doit en principe augmenter. Mais qu’au bout d’un moment, la performance en validation commence à décroitre, signe qu’il est temps d’arrêter l’entrainement pour éviter le surapprentissage.

Le grokking

Je vous remets maintenant la courbe dont on parle :

Cette courbe montre la performance en entrainement (en rouge) et en validation (en vert) d’un certain réseau de neurones au cours de son apprentissage. Je vous expliquerai bientôt d’où vient cette courbe, et la tâche qu’on cherchait à résoudre. Mais même sans cela, on voit que l’allure de cette courbe est en contradiction totale avec ce dont ont l’habitude les praticiens du machine learning !

Et notez bien l’échelle logarithmique pour les abscisses. Au bout quelques centaines d’étapes seulement, il est parfaitement clair que le modèle fait du sur-apprentissage à mort : sa performance est parfaite sur l’ensemble d’entrainement, et quasi-nulle sur l’ensemble de validation ! C’est le signe d’un modèle mal choisi et/ou mal entrainé. Et le bon sens voudrait qu’on arrête tout de suite la procédure d’entrainement, pour chercher par exemple un meilleur modèle.

Mais pour une raison que j’ignore, il semble que les auteurs de la publication aient laissé tourner ce modèle longtemps…très longtemps…très très longtemps…1000 fois plus longtemps que la période nécessaire à constater le sur-apprentissage ! Et un phénomène incroyable a fini par se produire : la performance sur l’ensemble de validation, et donc la capacité de généralisation du modèle, a finalement augmenté jusqu’à atteindre elle-aussi la quasi-perfection.

(Je ne peux pas m’empêcher de penser à un scénario de sérendipité façon “Flemming découvrant la pénicilline” : j’imagine les chercheurs oubliant d’arrêter leur modèle le soir en partant, et en revenant le lendemain matin pour découvrir cette courbe incroyable !)

Les chercheurs de la publication ont décidé de baptiser ce phénomène le “grokking”. C’est un mot d’argot difficile à traduire, qui a été inventé dans les années 60 par Robert Heinlein dans son roman de science-fiction En terre étrangère. Un mot qui est depuis passé dans le langage courant en anlais. To grok signifie en gros “comprendre complètement, de façon profonde et intuitive”. J’ai l’impression que les termes français qui s’en rapprochent le plus seraient “piger”, “saisir” ou encore “capter”. Dans la traduction du roman, c’est gnoquer qui est utilisé. Mais pour faire simple, je vais continuer à parler de grokking. C’est donc comme si soudainement, après des centaines de milliers d’étapes infructueuses, le modèle avait enfin fini par piger !

Mais l’histoire ne s’arrête pas à cette étrange courbe d’apprentissage : vous allez voir que de nouvelles surprises nous attendent quand on essaye de comprendre comment, et pourquoi, ce phénomène se produit.

Mais pour cela, il faut que je vous explique d’abord sur quel genre de tâche d’apprentissage les auteurs de la publication ont travaillé.

Une tâche simple, mais pas trop

Dans la publication d’origine, les chercheurs voulaient au départ étudier la possibilité d’utiliser des modèles d’IA sur ce qu’on appelle des jeux de données algorithmiques. Contrairement aux données qu’on trouve pour les applications de l’IA dans la “vraie vie”, il s’agit de jeux de données de taille modérée, et créés artificiellement à partir d’une procédure simple.

Une façon de le faire, c’est de fabriquer des jeux de données finis, en utilisant ce qu’on appelle l’arithmétique modulaire. Prenons un nombre P, par exemple P=12, et considérons deux entiers entre 0 et P-1, et calculons le résultat de leur addition modulo P, par exemple

6+9 = 3

3+11 = 2

4+8 = 0

3+6 = 9

L’idée est simple : on ajoute simplement les nombres, et si on atteint ou dépasse 12, on retire 12. Si cela vous parait bizarre comme opération, songez que c’est exactement ce qu’on fait avec les heures sur une horloge

S’il est 10h et que vous attendez pendant 5 heures, il sera ensuite … 3 heures ! Car 10+5 = 3 modulo 12. Retenez-bien cette image de l’horloge, on va en reparler !

On peut donc essayer de réaliser un modèle d’IA à qui on va donner des exemples d’opérations d’additions modulaire, et espérer que le modèle apprenne à les réaliser. Dit comme cela, ça semble très facile : évidemment qu’un réseau de neurones peut apprendre à faire des additions ! Mais attention, ce que nous allons lui donner en entrée et en sortie, ce ne sont pas des nombres, ce sont des tokens.

C’est-à-dire que rien dans la forme des données ne trahira le fait que nous sommes en réalité en train de manipuler des nombres, et qu’on effectue des opérations arithmétiques sur ceux-ci. Les données seront fournies au réseau sous la forme de paires de tokens en entrée, et d’un token “résultat” en sortie.

Imaginez par exemple que je considère un ensemble de 12 tokens, représentés chacun par un emoji, chacun de ces tokens représentant en fait secrètement un nombre entre 0 et 11.

😁🤣🙃🙂😀😆😊😅😂😇😃😄

Les données que je vais fournir à mon réseau de neurones seront du genre

Entrée : 😁🤣

Sortie : 🙂

Si je travaille avec un ensemble de 12 tokens, pour complètement spécifier une opération qui prend 2 tokens en entrée, j’ai 12x12 = 144 cas, que je peux écrire sous la forme d’une table, par exemple

Derrière cette table, il y a une opération d’addition modulaire sur les indices de chaque token. Mais présenté comme ça, sous forme d’une opération inconnue sur des tokens, c’est beaucoup moins apparent ! Et la tâche que l’on va demander à notre réseau de neurones, c’est d’apprendre à faire ces opérations sur les tokens uniquement à partir d’exemples qu’on va lui fournir.

Et c’est même encore pire, puisque du fait de la séparation entre ensemble d’entrainement et ensemble de validation, lors de son entrainement notre modèle ne verra pas toutes les combinaisons possibles. Il n’en verra par exemple que la moitié, et il devra complètement deviner les autres !

Dernière précision, là j’ai pris P=12 pour que ce soit facile à expliquer, mais dans la suite on va prendre des valeurs plus élevées, disons P=53. Vu du réseau de neurones, cela ressemble donc plutôt à ça : on vous file des données d’une table 53x53, et à vous de deviner ce qu’il y a dans les cases blanches !

Bref, nous parlons donc d’une catégorie de problèmes assez simple dans le sens où les données sont peu nombreuses, non-bruitées, et générées par une procédure algorithmique. Mais la tâche reste tout de même ardue pour un modèle, et probablement inenvisageable pour un humain (un humain à qui on n’aurait bien sûr pas révélé qu’il s’agit en fait d’arithmétique modulaire déguisée avec des tokens.)

Quel modèle utiliser ?

Passons à la pratique, et voyons quel modèle peut s’acquiter de cette tâche. L’architecture globale est la suivante

On l’a dit, en entrée notre modèle n’a aucune notion de nombre, la seule chose qu’il sache, c’est qu’on lui fournit des tokens, et qu’il y a P tokens différents. Vous êtes peut-être déjà familiers avec cette notion de token, qu’on retrouve aussi avec les modèles de langage. Pour des modèles comme GPT, un token est un mot ou une portion de mot que le modèle va “lire d’un coup”. Il ne lit pas les textes lettre par lettre, mais token par token.

Pour qu’un modèle puisse traiter un token, il faut d’abord convertir ce dernier en nombres, la seule chose que sachent manipuler nos réseaux de neurones. Le modèle va donc commencer par une opération qu’on appelle un embedding (“plongement” en bon français). L’idée est simple : à chaque token de notre ensemble, on va associer un vecteur dans un espace de dimension D. Le choix de la dimension est un paramètre du modèle, et on va le choisir en fonction de la complexité de la tâche et du nombre de tokens.

Les modèles de langage comme GPT commencent aussi par cette opération d’embedding. Ainsi par exemple le token “Chien” sera représenté par un certain vecteur dans un espace de grande dimension (plusieurs milliers), le token “Renard” par un autre vecteur, etc. Et le choix de ces vecteurs est fait librement par le réseau lors de son entrainement. En d’autres termes, les coordonnées des vecteurs de chaque token sont des poids du réseau. Le réseau va chercher tout seul à réaliser le meilleur embedding possible pour se faciliter la tâche par la suite.

Vous l’avez peut-être déjà lu, les embeddings réalisés par les modèles de langage possèdent des propriétés amusantes quand on les combine arithmétiquement. Par exemple si je prends les vecteurs associés aux embeddings des mots “Roi”, “Homme” et “Femme”, je peux réaliser l’opération

Roi - Homme + Femme

et je trouverai un vecteur qui se trouve très proche de l’embedding du token “Reine”. Ce qui semble indiquer que le modèle de langage a spontanément organisé les embeddings des tokens de manière à ce qu’ils reflètent une certaine sémantique de ces tokens.

Avec nos token-emojis qui représentent secrètement des entiers, nous allons faire pareil. A chaque token on associe un vecteur dans un espace d’embedding, et on laissera le réseau de neurones choisir ces vecteurs au cours de son entrainement.

Une fois cet embedding des tokens réalisé, il reste l’opération principale : prédire le token en sortie à partir de l’embedding des deux tokens en entrée.

Les premiers articles sur le sujet (dont celui d’OpenAI) utilisaient pour cela des transformers, qui sont en quelque sorte les unités de base qui composent les réseaux comme les modèles de langage. Comme il suffit à chaque fois de prendre seulement deux tokens en entrées, il s’agissait de “petits” transformers, beaucoup moins sophistiqués que ceux utilisés par exemple dans les modèles de langage.

De mon côté, j’ai voulu essayer de mettre en évidence le phénomène avec le réseau le plus simple possible, et j’ai réussi à le reproduire avec un simple réseau feedforward avec une couche cachée (plus de détails sur le github), je vous remets le schéma de l’architecture.

En sortie de ce réseau prédicteur, on récupère un vecteur de dimension P qui représente les probabilités de chacun des P tokens en sortie (plus précisément c’est un vecteur de logits, mais cela revient au même à notre niveau). Pour faire une prédiction, on choisit ensuite généralement le token le plus probable de la liste.

L’architecture est définie, il ne nous reste plus qu’à entrainer notre réseau ! Je vous passe les détails (à nouveau cf le github) mais notez qu’il ne se déroule pas de façon identique en fonction des choix faits notamment la quantité de données, le taux d’apprentissage, l’algorithme d’optimisation et la pénalité appliquée sur les poids.

Les résultats

Suivant les choix de la tâche à effectuer et des paramètres, le grokking se produit de façon plus ou moins tardive. L’exemple initial de la publication était avec la division modulaire, mais dans la suite je vais montrer les résultats de ma reproduction du phénomène dans un cas plus simple : l’addition modulaire.

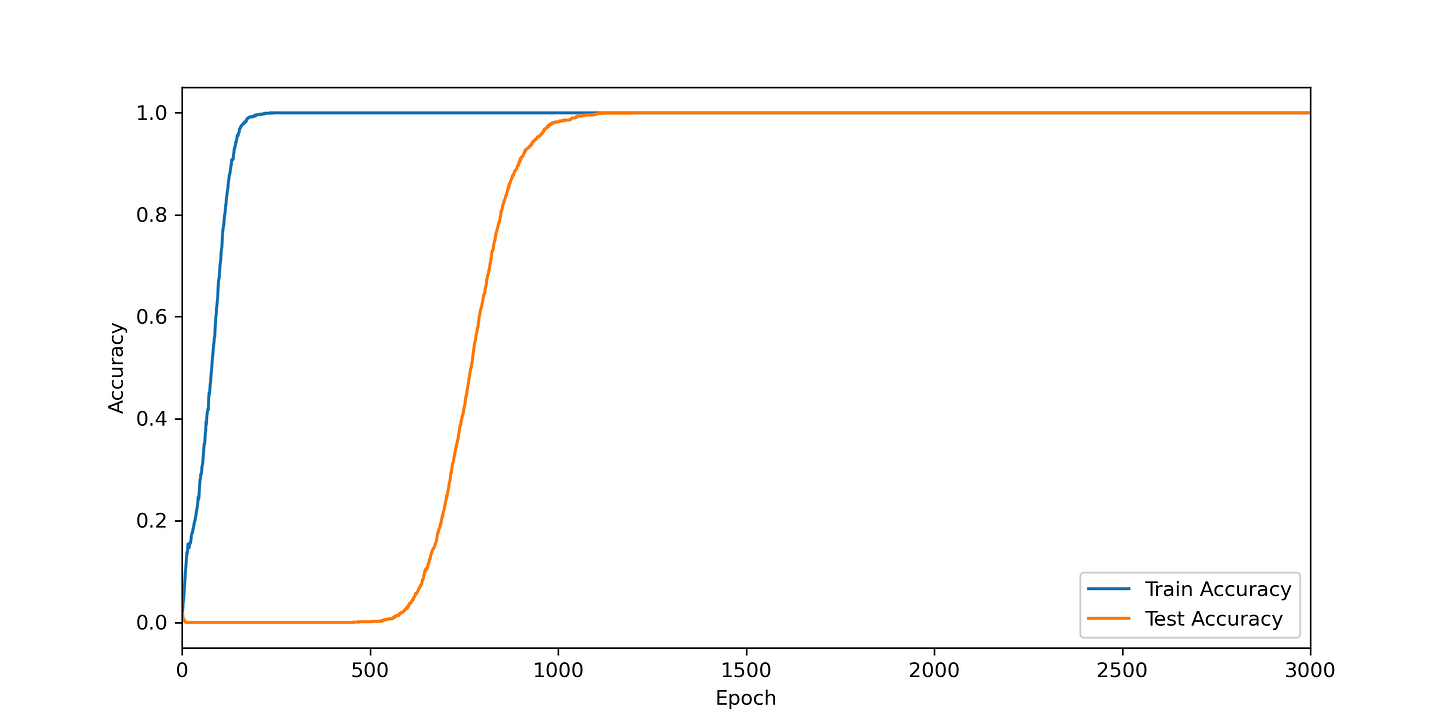
Avec l’addition modulo P=53 et mon choix d’architecture, voici ce que j’ai obtenu.

On voit très clairement le phénomène de grokking : la qualité de prédiction a rapidement atteint 100% pour l’ensemble d’entrainement (en bleu), tout en restant à zéro sur l’ensemble de validation (orange) : un sur-apprentissage total, donc, après environ 250 itérations. Avant que finalement la prédiction sur l’ensemble de validation ne décolle et atteigne à son tour 100% après environ 1000 itérations. La séparation entre les deux courbes est moins extrême que dans l’exemple initial, mais tout de même très nette.

Sur la courbe suivante on peut visualiser l’évolution de la fonction de perte (loss), qui contient plus d’information que la simple qualité de prédiction. Celle-ci mesure en quelque sorte à quel point le modèle est certain de sa prédiction, c’est-à-dire à quel point le vecteur des probabilités qu’il propose en sortie est concentré sur la bonne réponse.

On voit le même phénomène : initialement, la valeur décroit pour l’ensemble d’entrainement (bleu), au détriment de celle sur l’ensemble de validation (orange). Puis cette dernière finit par décroitre à son tour.

Et pour être parfaitement clair : souvenez-vous qu’à aucun moment le modèle et l’algorithme qui l’optimise n’ont connaissance de cette performance en validation (c’est le principe). Après un sur-apprentissage énorme, il finit par l’améliorer sans le savoir, et sans s’en rendre compte, et c’est ça qui est dingue !

Mais le plus beau reste à venir…car pour comprendre ce qu’il se passe, nous allons ouvrir les entrailles du modèle.

Un peu de neuro-imagerie artificielle

Vous vous souvenez que l’architecture de notre modèle commence par un module d’embedding, qui traduit chaque token en un vecteur dans un espace de grande dimension. Pour comprendre comment le modèle accomplit sa tâche, on peut essayer d’inspecter ces embeddings.

Je l’ai dit, l’espace d’embedding est un espace de très grande dimension : plusieurs milliers dans le cas des modèles de langage. Moi j’ai choisi un espace de dimension 128, mais cela reste bien trop pour espérer “visualiser” quelque chose directement. Il faut d’une façon ou d’une autre réduire la dimension pour pouvoir réaliser notre inspection.

Pour cela, la méthode la plus simple est de faire une analyse en composantes principales. C’est une méthode simple qui permet de projeter un espace de grande dimensions sur quelques composantes significatives. J’ai donc appliqué cette méthode sur les valeurs des embeddings de mon modèle entrainé, et voici le résultat si on prend les 12 premières composantes de la projection

Ce que vous voyez ici, ce sont des points qui représentent l’embedding de chaque token une fois projeté sur des paires de composantes principales. Je vous ai mis à côté de chaque point le nombre que représente secrètement le token (nombre que le modèle ignore, je le rappelle !!) Et ce qu’on y voit est absolument fou !

Pour créer son embedding, le modèle a naturellement structuré les données en cercles. Et regardez la figure centrale de la ligne du bas : c’est exactement comme une horloge avec 53 divisions ! Les autres figures représentent également des cercles mais avec une période différente, par exemple de 3 en 3 sur la figure en bas à droite. J’ai indiqué sur chaque graphique la fréquence que j’ai pu déceler.

Et pour redire les choses de façon parfaitement claire : le modèle n’a aucun moyen de savoir qu’il est en train de manipuler des entiers modulaires. Pour lui ce sont juste des tokens, et il a trouvé que le meilleur moyen de s’acquitter de sa tâche, c’était de les structurer ainsi. Et ce faisant, il a sans le savoir reproduit l’organisation en “horloge” qui fonctionne si bien pour faire de l’arithmétique modulaire !

(Petit complément pour ceux qui connaissent les analyses en composantes principales : les composantes suivantes ont une variance beaucoup plus faible).

Et c’est encore plus impressionnant quand on regarde l’évolution de l’embedding au cours des étapes d’entrainement, j’ai zoomé sur les composantes qui donnent des cercles de périodes 1 et 3

On voit peu à peu la structuration apparaître au fur et à mesure de l’apprentissage (ici j’ai laissé jusqu’à 20000 itérations), comme si le modèle découvrait peu à peu que cette manière de représenter les tokens était “la bonne”, celle qui lui permettrait d’être le plus performant possible.

J’ai joué un peu avec les différents paramètres du problème et du modèle, sans faire d’étude systématique de sensibilité. Mais dans les différents papiers consacrés au phénomène de grokking, on peut lire que le phénomène est robuste et se produit dans toute une variété de conditions.

Mais pourquoi les choses se produisent-elles de cette façon ? Que se passe-t-il à l’intérieur des neurones ? Certains chercheurs ont poussé plus loin l’exploration, et les découvertes sont fascinantes.

Comment le modèle fait-il ?

Nous avons vu que notre modèle avait découvert des embeddings permettant une structuration naturelle des tokens, qui reflète leurs propriétés sous-jacentes en arithmétique modulaire. Mais comment fait-il à partir de là pour réaliser l’opération d’addition modulo P ?

Une partie de la réponse se trouve dans ce papier :

NANDA, Neel, CHAN, Lawrence, LIBERUM, Tom, et al. Progress measures for grokking via mechanistic interpretability. arXiv preprint arXiv:2301.05217, 2023.

(Voir aussi cet excellent billet de blog par deux des auteurs)

En décortiquant le modèle entrainé, les chercheurs se sont rendu compte qu’il implémente une façon assez simple et naturelle de faire de l’addition modulaire. Je vous passe les détails mais cela fonctionne en trois étapes :

• Un embedding des tokens sous forme de cercles à différentes périodes (c’est ce qu’on a vu), c’est-à-dire que l’embedding représente des sinus ou des cosinus des nombres à additionner, avec une différentes “fréquences”. C’est une forme de transformée de Fourier discrète.

• Ensuite le prédicteur implémente des identités trigonométriques qui permettent de faire des additions de fonctions trigo, du genre cos(a+b) = cos(a)cos(b)-sin(a)sin(b)

• Et enfin il fait “interférer” les résultats obtenus avec les différentes fréquences, ce qui permet par interférences constructives de concentrer le logit sur la “bonne” réponse.

Ce qui est fascinant, c’est que cela revient en gros à faire l’addition modulaire grâce au principe de l’horloge ! Au cours de son entrainement, le modèle a découvert un algorithme simple et efficace de réaliser sa tâche (en faisant notamment une transformée de Fourier discrète lors de l’opération d’embedding)

Ensuite les chercheurs ont essayé de mesurer de quelle façon et à quel rythme cet algorithme apparaissait dans les neurones du réseau. Ils ont montré avec des métriques bien choisies que dans la phase initiale de sur-apprentissage, le réseau mémorise bêtement les exemples qui lui sont présenté. Puis que progressivement il établit des circuits neuronaux qui lui permettent de vraiment réaliser l’addition modulaire selon l’algorithme de l’horloge, et il finit par oublier sa mémorisation “par coeur” initiale.

Finalement, le réseau commence par apprendre bêtement, puis il finit par comprendre : il a pigé !

Je vous mets deux figures du papier qui illustrent ce qu’il se passe lors de l’entrainement, mais pour bien comprendre, allez plutôt le lire ! On voit à gauche l’évolution de différentes métriques de perte, et à droite les magnitudes des poids des différentes parties du modèle

Apparemment un ingrédient clé dans cette affaire, c’est la pénalité qui est appliquée sur les valeurs des poids pendant l’apprentissage. Au début de l’entrainement (jusqu’à 1K ci-dessus), le plus rentable est d’apprendre par coeur, quitte à impliquer des poids élevés. Et puis l’impact de la pénalité force le modèle à trouver des solutions plus intelligentes, ce qu’il finit par faire (entre 1K et 10K). Une fois l’algorithme découvert, il fait le ménage en supprimant les connexions qui lui avaient initialement permis de (sur-)apprendre par coeur (entre 9K et 13K).

Peut-être que je surinterprète de façon trop anthropomorphique, mais je trouve ça fascinant de voir que le modèle se comporte un peu comme nous : il apprend bêtement, puis il finit par comprendre, ce qui lui permet de stocker des représentations plus riches et plus compactes.

Pour aller plus loin…

Il y aurait encore beaucoup à dire sur le phénomène du grokking, et notamment un certain nombre de papiers de l’équipe de Max Tegmark au MIT, qui s’intéresse à ces questions d’interprétabilité des IA avec des outils de physique, et notamment de physique statistique. On y apprend notamment comment le phénomène du grokking peut-être vu comme une transition de phase, l’organisation des tokens dans l’espace d’embedding étant une sorte de cristallisation.

Un autre point intéressant est qu’une grande dimension d’embedding est nécessaire, pour faciliter le fait que le modèle trouve un bon sous-espace de représentation, même si à la fin (comme le montre l’analyse en composantes principales), tout se concentrera dans un sous-espace de faible dimension.

Je vous mets quelques références ci-dessous, et sans nul doute il y aura encore de nombreuses publications prochainement sur ce phénomène fascinant et inattendu ! Et n’hésitez pas à aller voir mon github pour voir comment j’ai essayé de reproduire le truc dans un cas minimal.

LIU, Ziming, KITOUNI, Ouail, NOLTE, Niklas S., et al. Towards understanding grokking: An effective theory of representation learning. Advances in Neural Information Processing Systems, 2022, vol. 35, p. 34651-34663.

Liu, Z., Michaud, E. J., & Tegmark, M. (2022). Omnigrok: Grokking beyond algorithmic data. arXiv preprint arXiv:2210.01117.

ZHONG, Ziqian, LIU, Ziming, TEGMARK, Max, et al. The Clock and the Pizza: Two Stories in Mechanistic Explanation of Neural Networks. arXiv preprint arXiv:2306.17844, 2023.